How KV Sparsity Achieves 1.5x Acceleration for vLLM

Zachary, Algorithm Expert at Novita AI 

Research Focus: Inference Acceleration

Introduction

Over the past year, since the emergence of H2O, there has been a proliferation of research papers on KV sparsity. However, one significant challenge in real-world applications is the substantial gap between academic research and practical implementation. For example, frameworks like vLLM adopt PagedAttention, a paging-based memory technique that is incompatible with most sparsity algorithms, or where these algorithms perform worse than PagedAttention. Such issues prevent sparsity algorithms from being effectively utilized in production environments.

By reviewing recent academic papers from the past year in the field of KV sparsity, we made modifications to the vLLM framework based on KV sparsity. These modifications were aligned with the inherent optimization features of the vLLM framework, such as Continuous Batching, FlashAttention, and PagedAttention. Ultimately, by comparing the modified framework against the SOTA inference frameworks, using the most commonly deployed models, parameters, and hardware in production, we achieved a 1.5x speedup in inference performance.

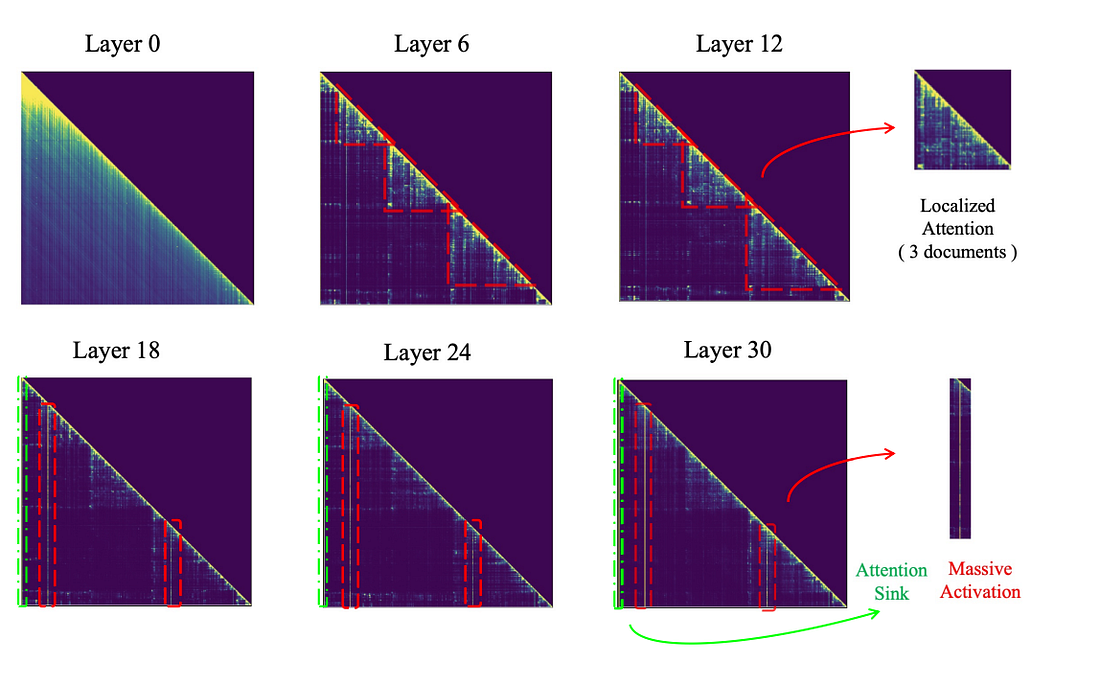
Before discussing KV sparsity, it is essential to address the characteristic of Massive Activations in LLMs. In LLMs, a small number of activation values are significantly more active than others, sometimes exceeding the less active ones by a factor of 100,000 or more. In other words, a small subset of tokens plays a critical role. This observation forms the basis for applying KV sparsity techniques, where retaining only the important tokens can enhance inference performance.

Specific analysis data from Llama2 and Llama3 further supports this observation, as shown in Fig. 1 and Fig. 2.

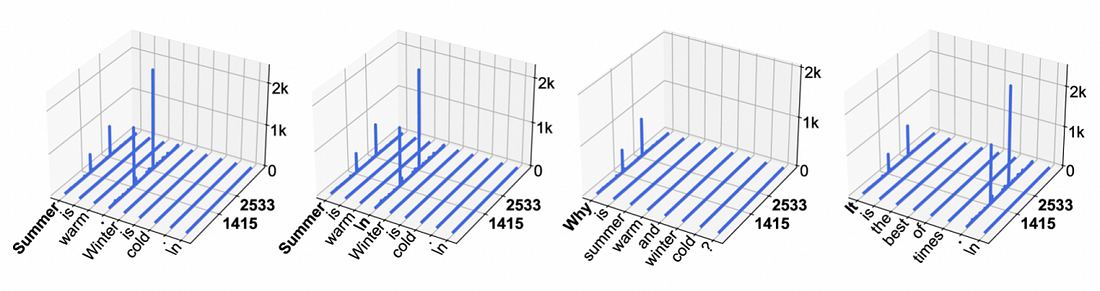
Unlike Llama2, Llama3 does not exhibit the Massive Activations characteristic across all layers. In the lower layers, activations are more uniformly distributed, while the middle layers display localized attention patterns. It is only in the upper layers that the Massive Activations phenomenon becomes prominent. This observation explains why models like Llama3 adopt hierarchical sparsity techniques, which tailor sparsity to different layers according to their specific activation patterns.

System Model

After introducing the Massive Activations characteristic in LLMs, we now have a basic understanding of the principles behind KV sparsity. Next, we will discuss how KV sparsity is implemented. In the inference process of large models, three major bottlenecks are commonly encountered: GPU memory capacity, computational power, and I/O bandwidth. To avoid redundant calculations, KV is often cached during inference, leading to significant consumption of GPU memory. Meanwhile, computational load and I/O throughput become critical bottlenecks in the Prefill and Decode stages, respectively.

Our modification of the vLLM framework is based on the Massive Activations characteristic of LLMs, implementing layer-wise sparsity (i.e., different levels of sparsity for different layers). This approach significantly reduces the overhead associated with KV caching, thereby accelerating the inference process of LLM models.

As shown in Fig. 3, during the inference process, we apply KV sparsity to different layers of the model. By employing a pruning strategy, we eliminate KV pairs with lower scores while retaining those with higher scores and closer proximity. This approach reduces memory usage, as well as computational and I/O overhead, ultimately leading to accelerated inference.

Inference Acceleration Results

The primary concern for most researchers is the actual impact of KV sparsity in the vLLM framework. Before delving into the details, we first present the performance evaluation results.

1.Inference performance

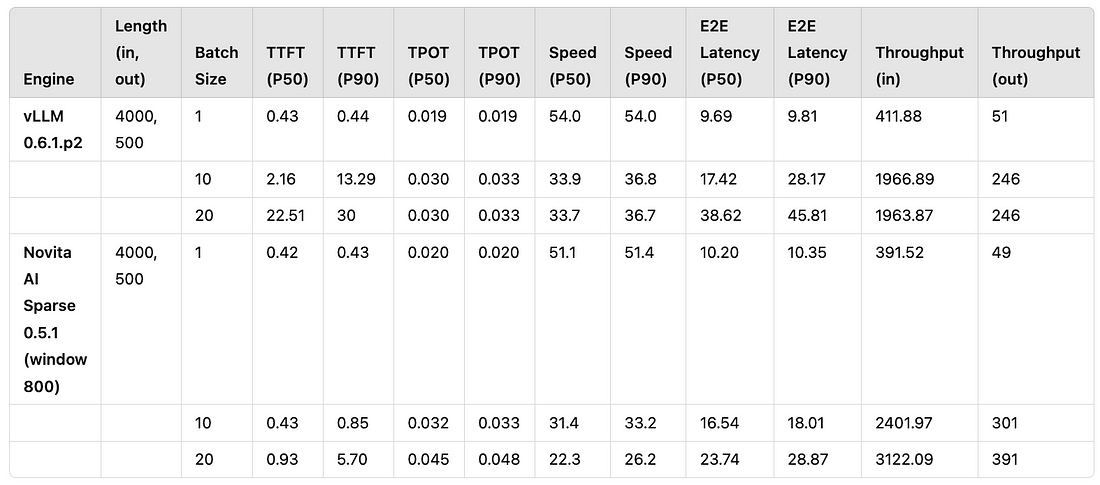
In real-world LLM applications, an input/output length of 4000/500 is the most commonly observed configuration. Additionally, the RTX 4090 GPU is one of the most widely used GPUs in the industry. Based on these conditions, we conducted batch performance comparison tests. The control group is vLLM 0.6.1.p2, while the experimental group is Novita AI Sparse 0.5.1 (a KV-sparsity-modified version of vLLM 0.5.1). Multiple rounds of performance comparison tests were carried out between the two, with key metrics including TTFT (time-to-first-token, critical for user experience) and Throughput (the actual inference speed).

The final test results are shown in Table 1. By applying KV sparsity, we were able to increase the throughput of vLLM by approximately 1.58x, while maintaining a usable TTFT (with P50 under 1 second). Additionally, under larger batch size scenarios, vLLM 0.6.1.p2 reached its performance limit at a concurrency level of 10, whereas Novita AI Sparse 0.5.1 was able to maintain stable TTFT performance even at a concurrency level of 20. This demonstrates the robustness of KV sparsity in ensuring performance stability in production environments.

Table 1：Performance Comparison between vLLM 0.6.1.p2 and Novita AI Sparse 0.5.1

2.Model Accuracy

Since KV sparsity is a lossy compression algorithm, it is equally important to evaluate the model’s performance. We conducted performance assessments based on Llama3–8B, including evaluations using MMLU and other benchmarks. The results indicate that the accuracy loss remains within approximately 3%.

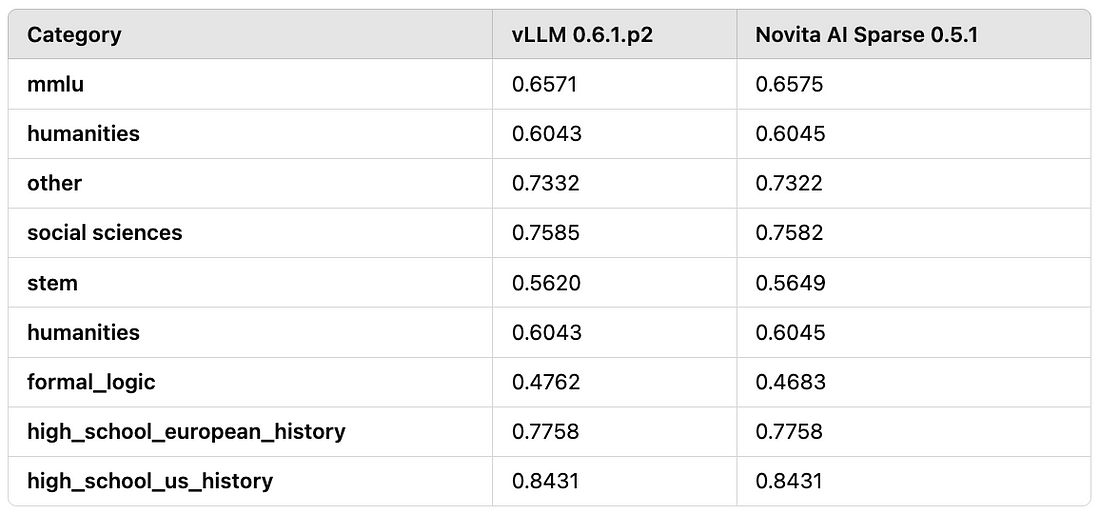
As shown in table 2, we tested the model performance using both MMLU and humanities benchmarks:

Table 2：Performance Evaluation Results of Llama3–8B using MMLU and Humanities Benchmarks

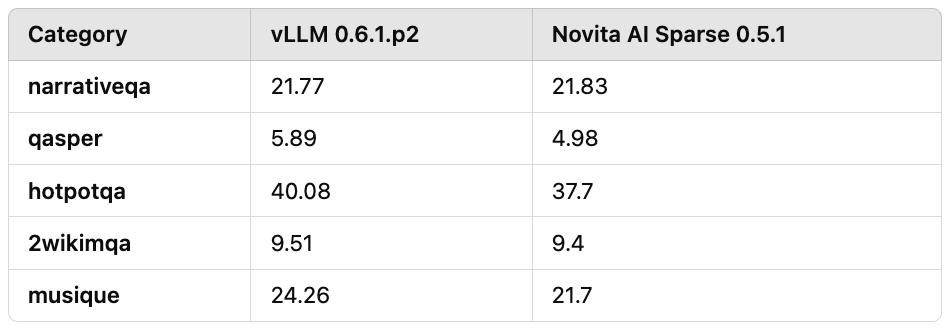
Secondly, we conducted evaluations of QA tasks in long text scenarios commonly encountered in practical applications, with input lengths ranging from 7k to 30k. The compression ratio was maintained at over 10 times, as shown in Table 3. The results indicated an overall accuracy loss of approximately 10%.

Table 3: Evaluation Results of Long Text QA Tasks with Input Lengths of 7k to 30k

Key Techniques

1.Layer-Specific Sparsity and Tensor Parallelism

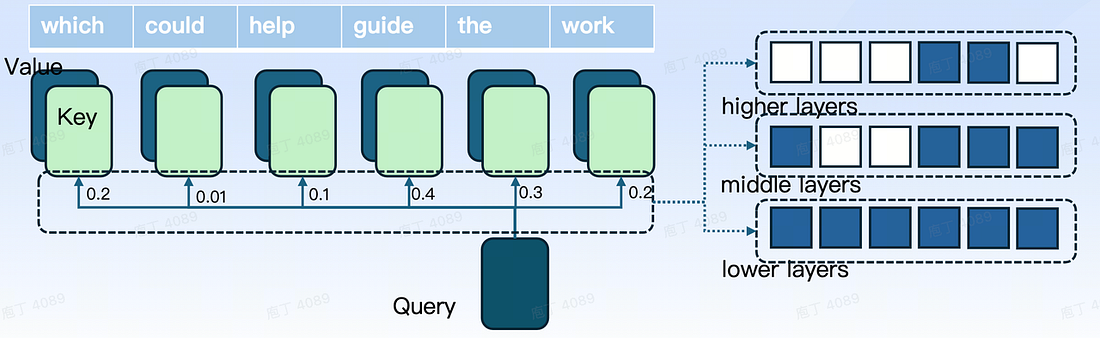
The vLLM framework employs an Iteration-Level Scheduling strategy, commonly referred to as Continuous Batching. This scheduling approach is characterized by not waiting for every sequence in a batch to complete generation; instead, it facilitates iteration-level scheduling, resulting in higher GPU utilization compared to static batching. As mentioned at the beginning of this paper, models like Llama3–8B inherently possess features such as hierarchical sparsity. Consequently, our modifications based on Continuous Batching have encountered a series of challenges as shown in Fig. 4.

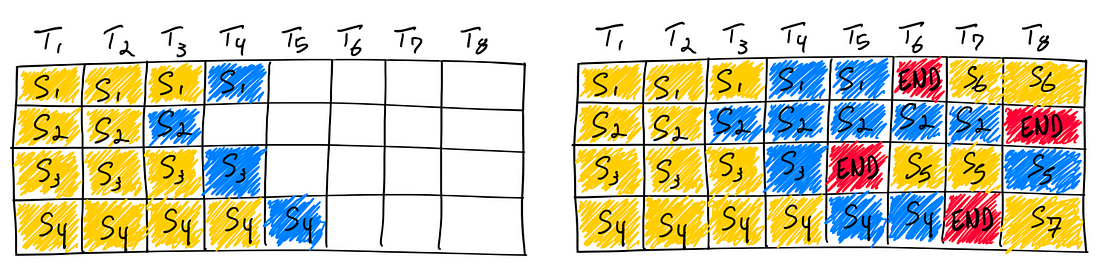
The primary challenge we tackled was the management of memory across diverse layers. Given vLLM’s utilization of a unified paging memory management model and the limitation of the queue strategy to only accommodate either Full Cache or Sliding Window, we made modifications to the core structure of vLLM to enable support for both options.

This adjustment grants each layer the flexibility to opt for either Full Cache or Sliding Window, allowing for distinct levels of sparsity across layers, as depicted in the diagram provided.

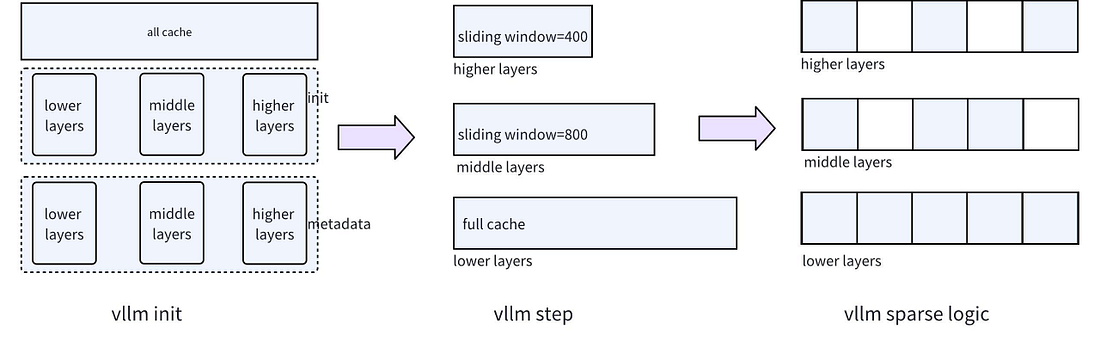
The first challenge to address is the memory management issue across different layers. Since vLLM utilizes a unified paging memory management model for all layers, and the queuing strategy allows for either Full Cache or Sliding Window, we need to adjust the underlying structure of vLLM. Specifically, this involves enabling support for both Full Cache and Sliding Window so that different layers can independently select their preferred memory management strategy. This adjustment ultimately facilitates varying degrees of sparsity across different layers. The corresponding structural diagram is shown in Figure 5.

Overall, the adjustments can be categorized into three distinct phases:

Service Initialization Phase: During the service startup process, the allocated memory for the three layers is initialized primarily through the calculation of the remaining space, alongside a hierarchical initialization of the Metadata structure. In contrast, the original vLLM operates as a complete Full Cache, without taking into account the memory allocation logic for different layers.

Step Preparation Phase: During the initialization process of the steps in vLLM, specifically in the phases involving block manager and model runner methods, different block table management strategies are employed for different layers to control the KV updating mechanism. As illustrated in the preceding figure, we utilize the Full Cache mechanism for the first three layers, storing all KVs, while layers beyond the third employ the Sliding Window strategy to automatically replace the KVs with the lowest scores. This approach allows for flexible allocation of memory space tailored to the needs of each layer, thus saving space while maximizing the effectiveness of the sparsity algorithm.

Sparsification Computation Phase: This phase typically occurs after model execution, where sparsity operations are executed based on the computed sparsity scores. A key consideration at this step is the compatibility with technologies such as Tensor Parallelism, CUDA graphs, and GQA. In practical engineering implementations, Tensor Parallelism requires particular attention. As illustrated in the figure below, in a single-machine multi-GPU scenario, it is essential to employ an appropriate partitioning mechanism to confine the KV sparsification operations within each GPU, thus avoiding communication between GPUs. Fortunately, the Attention unit employs a ColumnLinear-based partitioning approach, making its implementation relatively straightforward.

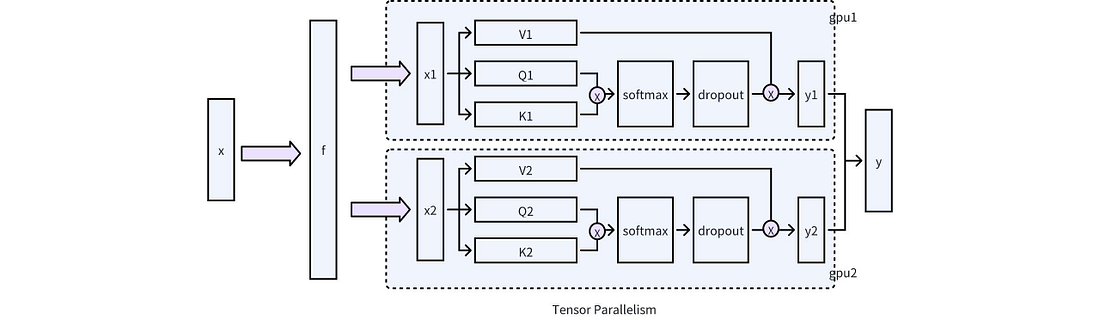
The above discussion primarily focuses on the modifications made at the framework level to support hierarchical sparsity in vLLM. Next, we will shift our attention to the optimizations implemented at the CUDA level.

2.Attention Modification

The modifications at the CUDA level primarily focus on the enhancements made to the Attention computation unit, specifically regarding FlashAttention and PagedAttention. While PagedAttention is relatively straightforward, we will emphasize the modifications related to FlashAttention.

First, we present the computation formula for Attention:

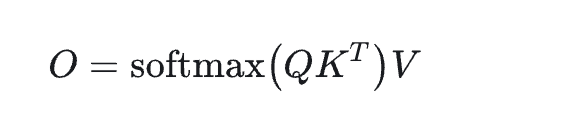
As shown in the formula, the softmax computation process involves calculating the product of QK, and it is a 2-pass algorithm (requiring two passes). However, the final computation target O can be achieved using the FlashAttention algorithm with a single pass (requiring one pass). The implementation logic of FlashAttention can be illustrated by the Fig. 7 from the FlashAttention2 paper. In brief, it involves chunk-wise traversal of Q to perform block calculations on KV, while gradually updating O, P and rowmax data until the loop concludes. Finally, dividing O by ℓ enables the 1-pass computation of FlashAttention.

For our implementation of KV sparsity, it is important to note that during the computation process of FlashAttention, the values required for softmax — namely, the rowmax/ℓ (the global maximum and cumulative values) are already computed. However, FlashAttention does not return the results of these two values.

With a foundational understanding of FlashAttention, we can now discuss the scoring formulas for sparsification presented in papers such as PYRAMIDKV:

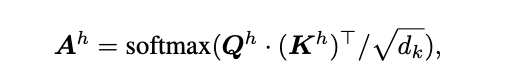
Specifically, we compute the score of selecting i-th token for retention in the KV cache as S in each attention head h by:

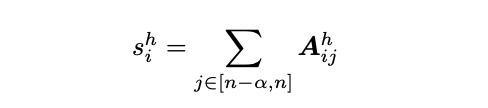
where [n − α, n] is the range of the instruction tokens. In each layer l and for each head h, the top k l tokens with the highest scores are selected, and their respective KV caches are retained. All other KV caches are discarded and will not be utilized in any subsequent computations throughout the generation process.

In the above formula, A represents the softmax score, while S denotes the sum of the scores of the a nearest softmax values. As indicated, softmax itself is a 2-pass algorithm, which cannot be directly integrated into FlashAttention. This also implies that the sparsification scoring cannot be implemented in 1-pass.

As previously mentioned, while FlashAttention does not output the softmax scores, it does compute intermediate values such as rowmax/ℓ. Therefore, by referencing the Online Softmax: 2-pass algorithm, we can utilize the outputs of rowmax/ℓ to achieve the specific scoring S for KV sparsity. In practice, we only need to make improvements to FlashAttention illustrated in Fig. 7 to meet this requirement.

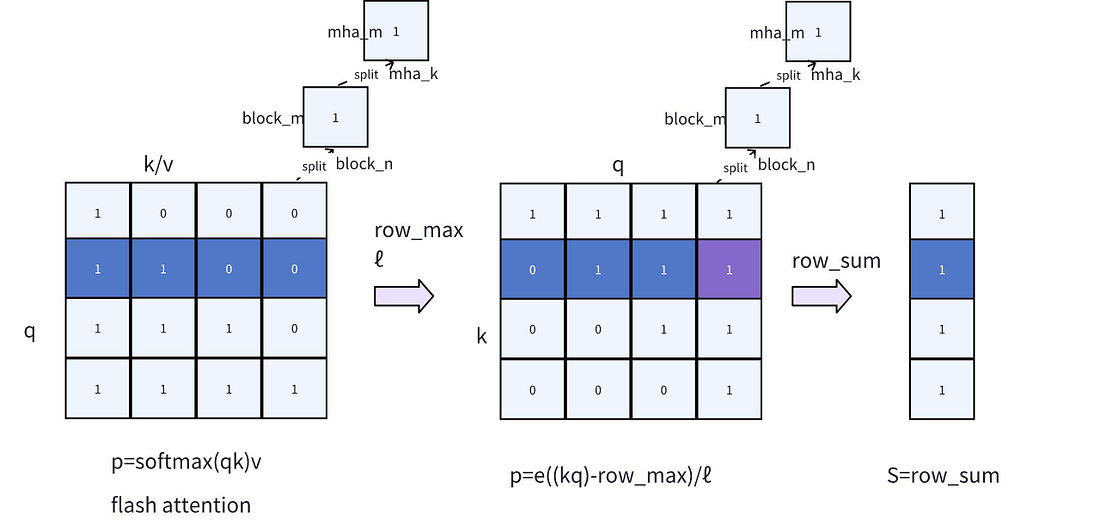
• Output of rowmax/ℓ in FlashAttention: FlashAttention incorporates the outputs of rowmax/ℓ. Since these values represent the maximum and cumulative totals, their data size is minimal, exerting negligible impact on the overall performance of FlashAttention. By reusing rowmax/ℓ, we can circumvent the need for a second 1-pass, thereby enhancing the overall computational efficiency.
• Addition of Online Softmax Step: We introduce the Online Softmax step, which builds upon FlashAttention by calculating the softmax scores using the formula p=e((kq)−row_max)/ℓ (1-pass logic). Subsequently, by performing a row-wise summation, we can compute the sparsification score S.

In the implementation of Online Softmax, two critical details require particular attention:

• Adjusting Loop Order: Since S is the summation of scores based on the k dimension, it is necessary to adjust the computation in Online Softmax from q*k to k*q, in comparison to the attention mechanism. This adjustment avoids unnecessary communication between different blocks by transforming the column summation into a row summation, allowing all computations to be completed within the registers.
• Start and End Positions of q: Due to the presence of causal encoding and the summation logic for the nearest a, it is unnecessary to traverse all q values with k. By referencing the mask indicators labeled as 0/1 in the Fig .7 , we can determine whether a corresponding block requires computation based on the starting and ending positions of q, which significantly conserves computational resources. For example, if the length of the input prompt is 5000 and the length of the nearest a is 256, the conventional computation would necessitate 5000*5000 operations. However, by recording the start and end positions, only 5000*256 operations are required, thereby enhancing computational efficiency.

PagedAttention performs work similar to that of FlashAttention, with the common goal of calculating the final score SSS. A detailed explanation of PagedAttention is not provided here.

Conclusion

Our modified version, Novita AI Sparse 0.5.1, based on vLLM 0.5.1, currently primarily supports models such as Llama3–8B and Llama3–70B. It operates in the inference mode using CUDA graphs and is primarily deployed on consumer-grade GPUs like the RTX 4090. There remains significant room for optimization both in engineering and algorithmic aspects.

Just a heads-up: The following features aren’t supported yet in vLLM-0.6.2:

• Chunked-prefill
• Prefix caching
• FlashInfer and other non-FlashAttention backends

For those interested in Novita AI Sparse 0.5.1, you can visit Novita AI to experience it ahead of others.

References:

[1] H2O: Heavy-Hitter Oracle for Efficient Generative Inference of Large Language Models

[2] Keyformer: KV Cache Reduction through Key Tokens Selection for Efficient Generative Inference

[3] SnapKV: LLM Knows What You are Looking for Before Generation

[4] PyramidKV: Dynamic KV Cache Compression based on Pyramidal Information Funneling

[5] PyramidInfer: Pyramid KV Cache Compression for High-throughput LLM Inference

[6] MiniCache: KV Cache Compression in Depth Dimension for Large Language Models

[7] Layer-Condensed KV Cache for Efficient Inference of Large Language Models

[8] TriForce: Lossless Acceleration of Long Sequence Generation with Hierarchical Speculative Decoding

[9] CacheBlend: Fast Large Language Model Serving for RAG with Cached Knowledge Fusion

[10] KV-Runahead: Scalable Causal LLM Inference by Parallel Key-Value Cache Generation