How Can Least-to-Most Prompting Enable Complex Reasoning in LLMs?
Introduction
What if language models could tackle complex problems with the same step-by-step approach humans use? In the realm of large language models (LLMs), the strategy of Least-to-Most Prompting offers a promising solution. Referencing the paper “Least-To-Most Prompting Enables Complex Reasoning in Large Language Models,” this blog explores how this innovative method enhances the reasoning capabilities of LLMs. By breaking down intricate tasks into manageable subproblems, Least-to-Most Prompting guides LLMs through a progressive sequence from simplicity to complexity.
What is Least-to-Most Prompting?
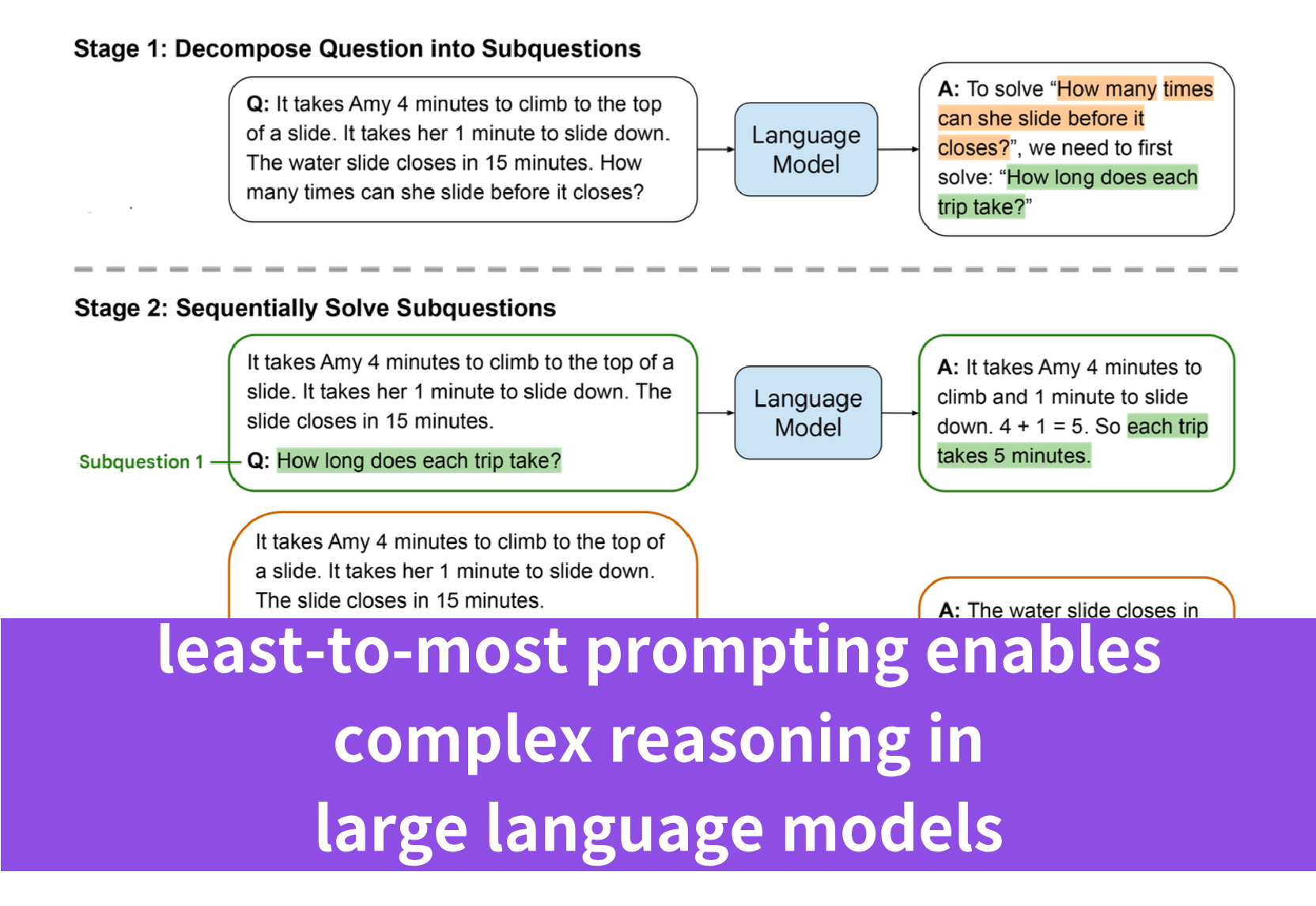
Least-to-most prompting is an innovative strategy introduced in the paper “Least-To-Most Prompting Enables Complex Reasoning in Large Language Models” to enhance the reasoning capabilities of large language models (LLMs). This method is designed to help LLMs tackle complex problems by breaking them down into a series of simpler, more manageable subproblems. The process involves two main stages:
- Decomposition: The complex problem is decomposed into a list of easier subproblems. This stage uses constant examples that demonstrate the decomposition process, followed by the specific question that needs to be broken down.
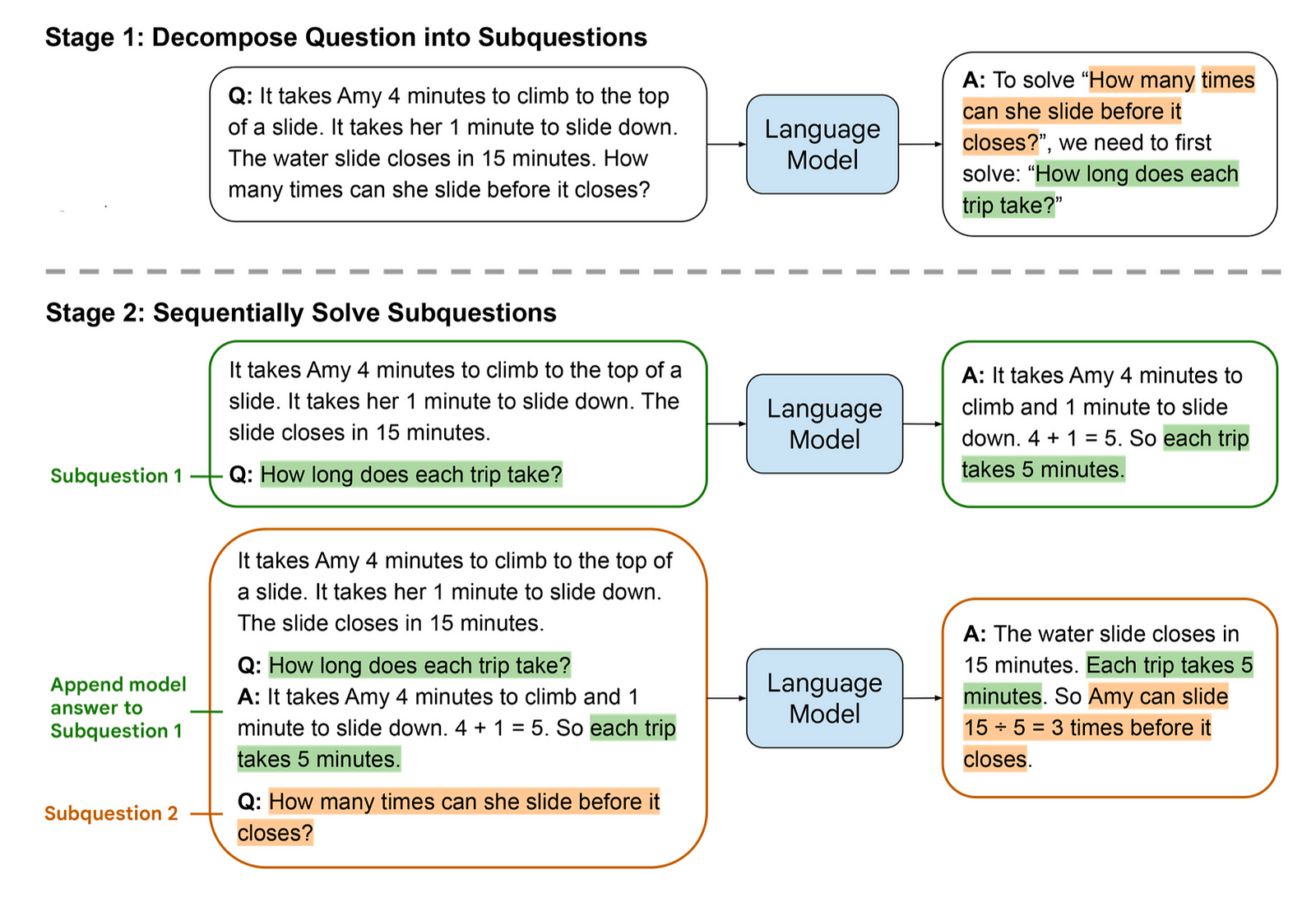
- Subproblem Solving: The model is then prompted to solve these subproblems sequentially. Each subproblem’s solution is facilitated by the answers to previously solved subproblems. This stage includes examples of how subproblems are solved, a list of previously answered subquestions and their solutions, and the next question to be addressed.
The prompts are constructed in a way that guides the model through a progressive sequence, from the simplest aspects of the problem to the most complex, hence the name “least-to-most.”
Why Do We Need Least-to-Most Prompting?
The need for least-to-most prompting arises from the limitations observed in existing prompting techniques, particularly chain-of-thought prompting.
Chain of thought prompting is an approach that encourages large language models to articulate their reasoning process step by step, similar to how a human would think through a problem. This method involves the model explicitly stating each logical step it takes to progress from understanding the question to reaching the final answer. By breaking down the problem into a series of intermediate reasoning steps, the model provides a transparent and justifiable solution path.
While chain-of-thought prompting has shown significant performance improvements for various natural language reasoning tasks, it tends to struggle when generalizing to solve problems that are more complex than the examples provided in the prompts.
How Can Least-to-Most Prompting Enable Complex Reasoning in LLMs?
The experiment design in the paper “Least-to-Most Prompting Enables Complex Reasoning in Large Language Models” can be broken down into the following step-by-step process:
Identify the Research Goal
The goal is to enable large language models to perform complex reasoning tasks that require solving problems more difficult than those demonstrated in the training examples.
Select the Tasks
The researchers chose tasks that are representative of different types of reasoning, including symbolic manipulation, compositional generalization, and mathematical reasoning.
Task 1: Symbolic Manipulation (Last-Letter Concatenation Task):
- Problem: Given a list of words, the task is to output the concatenation of the last letters of each word in the list.
- Example: For the input “think, machine, learning,” the correct output is “keg.”
- Least-to-Most Prompting:
- Decompose the problem: Break down the list into sequential sublists (“think,” “think, machine,” “think, machine, learning”).
- Solve subproblems: Concatenate the last letters of words in each sublist (“think” gives “k,” “machine” gives “e,” and “learning” gives “g”).
- Combine solutions: Use the solutions to the subproblems to construct the final answer (“k” + “e” = “ke” and “ke” + “g” = “keg”).
Task 2: Compositional Generalization (SCAN Benchmark):
- Problem: Map natural language commands to action sequences. The challenge is to generalize to longer action sequences than those seen during training.
- Example: The command “look opposite right thrice after walk” should be translated to the action sequence “TURN RIGHT, TURN RIGHT, LOOK, WALK.”
- Least-to-Most Prompting:
- Decompose the command: Break down the complex command into simpler parts (“look opposite right thrice” and “walk”).
- Map to actions: Translate each part into actions (“look opposite right thrice” becomes “TURN RIGHT, TURN RIGHT, LOOK” repeated thrice, and “walk” remains “WALK”).
- Combine actions: Sequentially execute the actions to form the final sequence.
Task 3: Mathematical Reasoning (GSM8K and DROP Datasets):
- Problem: Solve math word problems that may require multiple steps of reasoning.
- Example: “Elsa has 5 apples. Anna has 2 more apples than Elsa. How many apples do they have together?”
- Least-to-Most Prompting:
- Decompose the problem: Identify the subproblems (How many apples does Anna have? How many apples do they have together?).
- Solve subproblems: Calculate Anna’s apples (5 + 2 = 7) and then the total (5 + 7 = 12).
- Final answer: Conclude that Elsa and Anna have 12 apples together.
Design the Prompting Strategies
Two main prompting strategies are compared:
- Chain-of-Thought Prompting: This involves providing the model with examples that demonstrate a step-by-step reasoning process to solve a problem.

- Least-to-Most Prompting: This novel strategy involves breaking down a complex problem into simpler subproblems and solving them sequentially, using the solutions to previous subproblems to facilitate the solution of the next.

Create Prompt Examples
For each prompting strategy, the researchers crafted examples that demonstrate how to approach the tasks. For least-to-most prompting, this includes examples of both problem decomposition and subproblem solving.
Implement the Prompting in the Model
The language model is then given these prompts as input. For least-to-most prompting, this involves two stages:
- Decomposition Stage: The model is asked to break down the original problem into a series of simpler subproblems.
- Subproblem Solving Stage: The model is then asked to solve these subproblems sequentially, using the answers from previous subproblems to inform the solution of the next.
Construct the Test Sets
For each task, the researchers created test sets with varying levels of difficulty.
Task 1: Symbolic Manipulation (Last-Letter Concatenation Task):
- The test set for this task involved generating lists of words with varying lengths to test the model’s ability to concatenate the last letters of each word in the list.
- The researchers used a list of the 10,000 most common English words from Wiktionary, excluding profane words, resulting in a list of 9,694 words.
- For each desired list size (ranging from 4 to 12 words), they generated 500 random sequences of these words. Each sequence served as an input, and the corresponding output was the sequence of last letters of the words.
Task 2: Compositional Generalization (SCAN Benchmark):
- The SCAN benchmark consists of natural language commands that need to be mapped to action sequences. The test set challenges the model to generalize from shorter to longer action sequences.
- The researchers used the existing splits of the SCAN dataset, particularly focusing on the length split, which contains action sequences longer than those in the training set.
- They also ensured that the test set covered a range of commands to evaluate the model’s ability to handle different types of compositional generalization.
Task 3: Mathematical Reasoning (GSM8K and DROP Datasets):
- For mathematical reasoning, the researchers used word problems from the GSM8K dataset and the numerical reasoning subset of the DROP dataset.
- The test set included problems that required varying numbers of reasoning steps to solve, allowing the researchers to evaluate how well the model could generalize from simpler to more complex problems.
- The problems were selected to represent a range of difficulty levels and to ensure that some problems required more steps than those demonstrated in the prompts.
By constructing test sets in this manner, the researchers were able to rigorously evaluate the least-to-most prompting strategy and compare its effectiveness against standard prompting techniques across different reasoning tasks.
Run Experiments and Collect Results
The researchers ran experiments using the GPT-3 model (specifically the code-davinci-002 version) with both prompting strategies. They recorded the accuracy of the model’s responses on the test sets.
Analyze the Results
The researchers compared the performance of the model using different prompting strategies. They looked at overall accuracy and also broke down the results by the number of reasoning steps required to solve the problems.
Error Analysis
For least-to-most prompting, the researchers conducted a detailed error analysis to understand common mistakes, such as incorrect decomposition of problems or incorrect solving of subproblems.
How Much Better Are LLMs’ Performance With Least-To-Most Prompting?
The paper “Least-To-Most Prompting Enables Complex Reasoning in Large Language Models” demonstrates the effectiveness of least-to-most prompting across various tasks and compares its performance with chain-of-thought prompting and standard prompting methods. Here’s a summary of the performance improvements for each task as detailed in the paper:
Symbolic Manipulation (Last-Letter Concatenation Task):
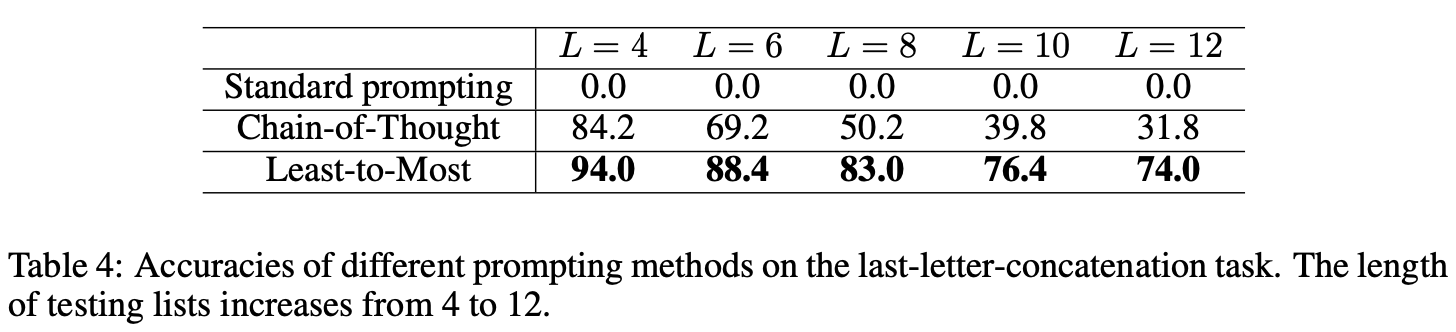
The least-to-most prompting significantly outperformed chain-of-thought prompting, especially when the length of the word lists increased.
For lists with lengths ranging from 4 to 12 words, the accuracy of least-to-most prompting with the GPT-3 code-davinci-002 model ranged from 74.0% to 94.0%, which was substantially higher than the accuracy of chain-of-thought prompting, which ranged from 31.8% to 84.2%.
Compositional Generalization (SCAN Benchmark):
Least-to-most prompting achieved an accuracy of 99.7% under the length split condition using only 14 exemplars, which is a remarkable result considering that specialized neural-symbolic models trained on the entire dataset of over 15,000 examples often struggle with this task.
In contrast, chain-of-thought prompting achieved only 16.2% accuracy with the same model on the length split condition.
Mathematical Reasoning (GSM8K and DROP Datasets):
On the GSM8K dataset, least-to-most prompting slightly improved over chain-of-thought prompting, with an overall accuracy of 62.39% compared to 60.87% for chain-of-thought prompting.
However, for problems requiring at least 5 steps to solve, least-to-most prompting showed a significant improvement, with an accuracy of 45.23% compared to 39.07% for chain-of-thought prompting.
On the DROP dataset, least-to-most prompting outperformed chain-of-thought prompting by a large margin, with accuracies of 82.45% and 74.77% for non-football and football subsets, respectively, compared to 58.78% and 59.56% for chain-of-thought prompting.
These results indicate that least-to-most prompting is particularly effective in tasks that require the model to generalize from simpler examples to more complex problems. The strategy of breaking down complex problems into a series of simpler subproblems and solving them sequentially allows the model to achieve higher accuracy rates across different reasoning tasks.
How to Integrate Least-To-Most Prompting to My Own LLM?
Based on the approaches presented by the authors of “Least-To-Most Prompting Enables Complex Reasoning in Large Language Models”, we create this step-by-step guide for you:
Step 1: Obtain an LLM API
First, you need to have access to an LLM that you can use for your task. Novita AI LLM API provides developers with many cost-effective LLM options, including Llama3–8b, Llama3–70b, Mythomax-13b, etc.
Here’s an example of making a Chat Completion API call with Novita AI LLM API:
from openai import OpenAI
client = OpenAI(
base_url="https://api.novita.ai/v3/openai",
# Get the Novita AI API Key by referring: https://novita.ai/get-started/Quick_Start.html#_3-create-an-api-key
api_key="<YOUR Novita AI API Key>",
)
model = "Nous-Hermes-2-Mixtral-8x7B-DPO"
stream = True # or False
max_tokens = 512
chat_completion_res = client.chat.completions.create(
model=model,
messages=[
{
"role": "system",
"content": "Act like you are a helpful assistant.",
},
{
"role": "user",
"content": "Hi there!",
}
],
stream=stream,
max_tokens=max_tokens,
)
if stream:
for chunk in chat_completion_res:
print(chunk.choices[0].delta.content or "", end="")
else:
print(chat_completion_res.choices[0].message.content)Step 2: Prepare the Prompt for Decomposition
Create a set of example prompts that demonstrate how to decompose a complex problem into a series of simpler subproblems. The examples should show the structure of the decomposition, but not necessarily the specific content of the subproblems.
Step 3: Prepare the Prompt for Subproblem Solving
Create a set of example prompts that demonstrate how to solve the individual subproblems. These examples should show the process of building the solution step-by-step, using the results of previously solved subproblems.
Step 4: Implement the Least-to-Most Prompting Algorithm
The key steps in the Least-to-Most Prompting algorithm are:
a. Pass the original problem to the decomposition prompt and obtain the list of subproblems.
b. For each subproblem, construct a prompt that includes the previous subproblem solutions (if any) and the current subproblem, and pass it to the LLM to obtain the solution.
c. Combine the solutions to the subproblems to obtain the final solution to the original problem.
Step 5: Integrate with Your Application
Incorporate the Least-to-Most Prompting algorithm into your application’s workflow. This may involve preprocessing the input, constructing the prompts, calling the LLM API, and postprocessing the outputs.
Step 6: Evaluate and Iterate
Test your implementation on a variety of tasks and problem difficulties. Analyze the errors and refine your prompt design or the prompting algorithm as needed.
This is a high-level example created by LLM, and you may need to adapt it to your specific use case and LLM.
import openai
# Set the Novita AI API key
openai.api_key = "<YOUR Novita AI API Key>"
openai.base_url = "https://api.novita.ai/v3/openai"
def decomp_prompt(original_problem):
"""
Generates a prompt to decompose the original problem into a series of subproblems.
Args:
original_problem (str): The original problem to be decomposed.
Returns:
str: The prompt for decomposing the problem.
"""
return f"""
Please decompose the following problem into a series of subproblems that can be solved step-by-step:
{original_problem}
Subproblems:
{{{decomp_steps}}}
"""
def solve_prompt(prev_solutions, subproblem):
"""
Generates a prompt to solve a specific subproblem, given the previously solved subproblems.
Args:
prev_solutions (str): The previously solved subproblems.
subproblem (str): The subproblem to be solved.
Returns:
str: The prompt for solving the subproblem.
"""
return f"""
Given the following previously solved subproblems:
{prev_solutions}
Please solve the following subproblem:
{subproblem}
"""
def solve_problem(original_problem):
"""
Solves the original problem using the Least-to-Most Prompting algorithm.
Args:
original_problem (str): The original problem to be solved.
Returns:
list: A list of solutions for the subproblems.
"""
# Decompose the original problem into subproblems
decomp_result = openai.Completion.create(
engine="text-davinci-002",
prompt=decomp_prompt(original_problem),
max_tokens=1024,
n=1,
stop=None,
temperature=0.7,
)
decomp_steps = decomp_result.choices[0].text.strip()
# Solve the subproblems one by one
solutions = []
for step in decomp_steps.split("\n"):
step = step.strip()
if step:
solve_result = openai.Completion.create(
engine="text-davinci-002",
prompt=solve_prompt("\n".join(solutions), step),
max_tokens=1024,
n=1,
stop=None,
temperature=0.7,
)
solutions.append(solve_result.choices[0].text.strip())
return solutions
# Example usage
original_problem = "Solve a complex math problem step-by-step."
solutions = solve_problem(original_problem)
print("\n".join(solutions))What Are the Limitations of Least-To-Most Prompting?
Domain-Specificity:
Decomposition prompts are often tailored to specific domains and may not generalize well across different types of problems. A prompt that works well for mathematical word problems may not be effective for common sense reasoning problems or those in other domains.
Intra-Domain Generalization Challenge:
Even within the same domain, generalizing the decomposition process can be difficult. The prompts need to be carefully designed to demonstrate the correct decomposition for the model to achieve optimal performance.
Complexity of Decomposition:
Some complex problems may require a sophisticated understanding of how to break them down into simpler subproblems. Designing prompts that effectively guide the model through this process can be challenging.
Sequential Dependence:
The subproblems generated in least-to-most prompting are often dependent and need to be solved in a specific order. This sequential requirement can make the prompting process more complex compared to independent subproblems.
Error Propagation:
If the model makes an error in the early stages of problem decomposition or subproblem solving, this error can propagate through the subsequent steps, leading to an incorrect final solution.
Model-Specific Performance:
The performance of least-to-most prompting can vary between different models or versions of the same model. Some models may be better suited to handle the iterative and recursive nature of the task.
Prompt Engineering:
The effectiveness of least-to-most prompting may rely heavily on the quality of prompt engineering. Creating effective prompts that lead to accurate decomposition and solution generation requires careful consideration and expertise.
Scalability:
While least-to-most prompting can be effective, it may not scale as well to very large or highly complex problems due to the increased difficulty in designing appropriate prompts and the potential for error propagation.
Lack of Bidirectional Interaction:
The authors suggest that prompting, in general, might not be the optimal method for teaching reasoning skills to LLMs because it is a unidirectional communication form. A more natural progression could involve evolving prompting into fully bidirectional conversations that allow for immediate feedback and more efficient learning.
Conclusion
By decomposing complex problems into simpler steps and solving them sequentially, LLMs with Least-to-Most Prompting not only enhance their reasoning but also demonstrate remarkable performance across various tasks — from symbolic manipulation to compositional generalization and mathematical reasoning.
However, it’s important to acknowledge the challenges that accompany this method. Domain-specificity, intra-domain generalization difficulties, and the complexity of decomposition can present hurdles. Moreover, the sequential dependence of subproblems and potential error propagation underscore the need for careful prompt engineering and model-specific considerations.
As we continue to explore new frontiers in AI development, Least-to-Most Prompting stands out as a pivotal strategy that empowers LLMs to navigate the challenges of complex reasoning tasks with unprecedented accuracy and efficiency, while also prompting ongoing research into optimizing its application across diverse problem domains.
References
Zhou, D., Schärli, N., Hou, L., Wei, J., Scales, N., Wang, X., Schuurmans, D., Cui, C., Bousquet, O., & Chi, E. (2023). Least-to-Most Prompting Enables Complex Reasoning in Large Language Models. In Proceedings of the International Conference on Learning Representations.
Novita AI is the all-in-one cloud platform that empowers your AI ambitions. With seamlessly integrated APIs, serverless computing, and GPU acceleration, we provide the cost-effective tools you need to rapidly build and scale your AI-driven business. Eliminate infrastructure headaches and get started for free — Novita AI makes your AI dreams a reality.